En ABEHA tenemos el placer de colaborar con personas de ciencia que hacen una grandiosa labor en el ramo de la ingeniería. Uno de esos colaboradores es el M. en C. Rodolfo Vera Amaro, que hoy en día se encuentra en en cuarentena en el estado Virginia, Estados Unidos haciendo una estancia de investigación .
La preocupación del maestro Rodolfo ante la situación actual, lo ha llevado a investigar una manera de hacer predicciones de comportamiento del COVID-19, para informar a la sociedad de la importancia del aislamiento y minimizar la fuerza de contacto.
A continuación te dejamos el documento de su investigación.
ANÁLISIS DE DATOS DEL COVID-19 Y PREDICCIÓN DE CASOS A NIVEL MUNDIAL USANDO EL MODELO SEIR MODIFICADO
Cada vez más rápido el COVID-19 se esparce a nivel mundial, principalmente en los países de Europa como en Estados Unidos. Al ser un virus desconocido y de rápido contagio, cada día es fundamental para los países que ya están en estado crítico o están por empezar la infección en la población, el tratar de prevenir y prepararse ante esta declarada pandemia por la Organización Mundial de la Salud [1] el pasado 30 de Enero del 2020 , de acuerdo a las características del virus, que a la fecha, todavía se siguen actualizando, como pueden ser: la fuerza de contagio, el número de reproducción o llamado también el número , el tiempo de incubación y el tiempo de la infección, es decir, el tiempo en que el enfermo tarda en recuperarse o en su caso, morir.
Debido a la numerosa desinformación que ha estado circulando en los medios de comunicación así como en las redes sociales y la necesidad conocer escenarios posibles, no sólo por la población, sino por los gobiernos de cada país y líderes del mundiales, este este artículo ofrece datos esenciales sobre el comportamiento del llamado COVID-19 o Coronavirus, así como de analizar e implementar un modelo modificado tradicional llamado SEIR (acrónimo de susceptibles, expuestos, infectados y removidos) [2] para predecir el número de personas susceptibles (S), expuestas (E), infectadas (I), y removidos (R) en una población determinada y los resultados se validan con los datos reales de países en los que la enfermedad se ha controlado o está en estado crítico de crecimiento (a la fecha de publicación de este artículo).
INTRODUCCIÓN
Muchos trabajos se han desarrollado para modelar y predecir el efecto en la población de las epidemias y pandemias como el SARS [3], Ébola [4], H1N1 [5], entre otros a lo largo de los años, pero esta al ser una enfermedad nueva no hay mucho trabajo relacionado y a la fecha se siguen publicando artículos científicos [6, 7, 8, 9, 10].

Este trabajo se basa en el modelo modificado propuesto en [2], el cuál propone introducir el parámetro de distanciamiento social y hacemos el análisis de los datos extraídos de la base de datos que se muestran en worldometers.com [10] de los países con más casos (a la fecha de publicación de este estudio), como son China o Corea del Sur, para tomarlos de referencia para calcular y ajustar parámetros utilizados. Además, se muestran los resultados del número de casos infectados y expuestos del modelo comparando y validándolos con los resultados de los datos reales de los países más representativos de la enfermedad y en México (este estudio puede extenderse a otros países).
MODELO SEIR
El modelo denominado SEIR, es un modelo epidemiológico simple, bien conocido y sencillo de implementar, el cuál utiliza parámetros característicos propios del COVID-19 el cuál implementaremos y simularemos en Matlab. El modelo SEIR se utiliza para conocer cómo una enfermedad se propaga a través de una población a través de fases S, E, I y R, donde las personas pasan de una de estas fases a la siguiente. Cuando alcanzan el estado R, ya no pueden infectarse, y según la interpretación es que sobrevivieron a la enfermedad y ahora son inmunes o sucumbieron ante la enfermedad y se consideran que ya están fuera de la fase de personas S. El modelo está dado por cuatro ecuaciones diferenciales de primer orden (EDO) con respecto al tiempo definido por
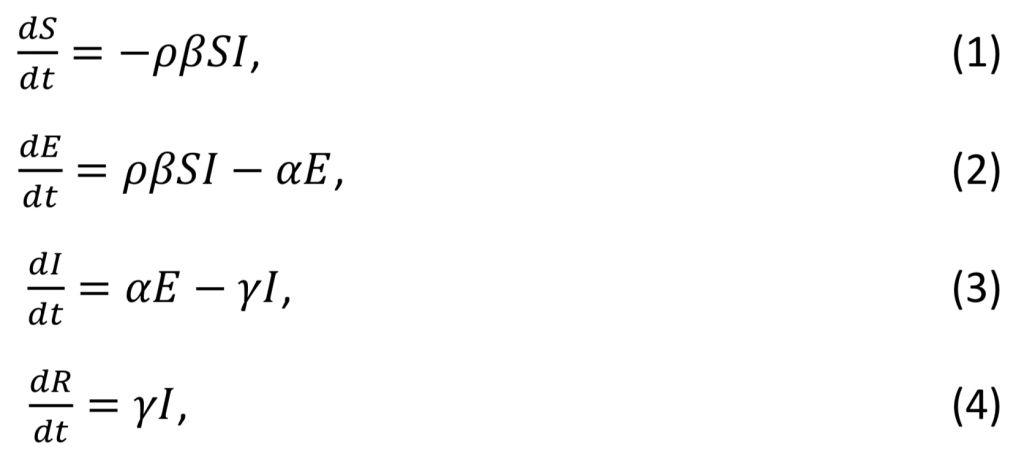
donde 𝛼 es la inversa del tiempo de incubación \left ( \frac{1}{^{t}incubación} \right ) , 𝛽 es el promedio de la tasa de contacto entre la población, 𝛾 es la inversa del periodo de infección o recuperación esperado \left ( \frac{1}{^{t}infección} \right ), 𝑁 = 𝑆 + 𝐸 + 𝐼 + 𝑅 con 𝑁 como el tamaño de la población y 𝜌 es la constante de separación social; dicha constante se refiere a que si 𝜌 es cercano a 1, no hay distanciamiento entre las personas y 𝜌 cercano a cero, hay mucho distanciamiento social. Además, existe una forma en que los expertos abordan el problema de la intensidad de contagio de una enfermedad, es calculando al denominado número de reproducción R_{0} definido por

La ecuación (1) describe a las personas susceptibles a la enfermedad (cada vez menos si hay cada vez más infectados) con respecto al tiempo y está condicionado por el número de personas infectadas y su contacto con los infectados. La ecuación (2) proporciona a las personas que han estado expuestas al virus. La ecuación (3) representa el cambio en el tiempo de las personas infectadas en función de la población expuesta y el período de incubación. Disminuye según el período de infección, por lo que cuanto mayor sea, más rápido mueren o se recuperan las personas y pasará a la ecuación (4). Tenemos una población fija de principio a fin.
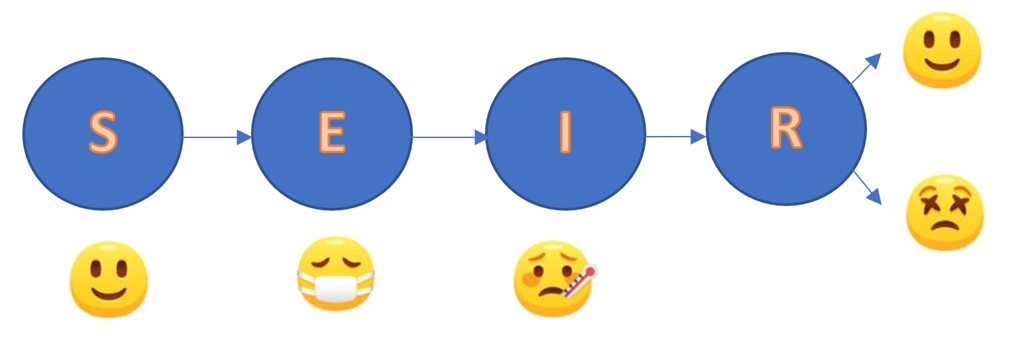
Fig. 3.- Fases de las personas de acuerdo al modelo SEIR. Susceptibles, Expuestos, Infectados y Removidos (Recuperados/Muertos).
Resultados numéricos
Para hacer la simulación se utilizó un lenguaje de programación como Matlab© que puede resolver las ecuaciones diferenciales y graficar los resultados obtenidos. Los parámetros se obtuvieron como:
- la tasa de incubación
𝛼 de acuerdo a [10], es la inversa de 6 días,
- la tasa de removidos
𝛾, la obtuvimos de los datos publicados por [10] de aproximadamente 5 días,
- la fuerza de contagio se calculó con la ecuación (5), utilizando R_{0}=3.5 y R_{0}=15
ya que en [9] se estima que es de 4.2
pero en [11], consideran que para enfermos con síntomas que estarán en cuarentena es de
R_{0}=3 y R_{0}=15
para personas sin síntomas que no están en cuarentena),
- y el valor de 𝜌
lo variamos de mayor distanciamiento a menor distanciamiento.
En las Fig. 4a-14a, se muestran los resultados del número de infectados con respecto a los días, del modelo y los datos reales (actualizados hasta el día 31 de Marzo 2020) para China, Corea del Sur, Irán, Italia, España, Italia, Estados Unidos, Alemania, Francia y México con 𝜌 = 0.25, 0.5, 0.75 𝑦 1; en las Figs. 4b-14b con
R_{0}=15. además de que las gráficas se normalizaron al inicio del brote real.
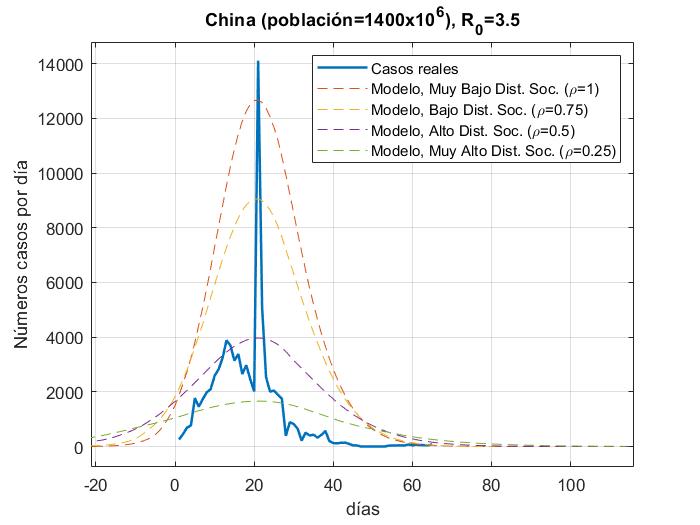
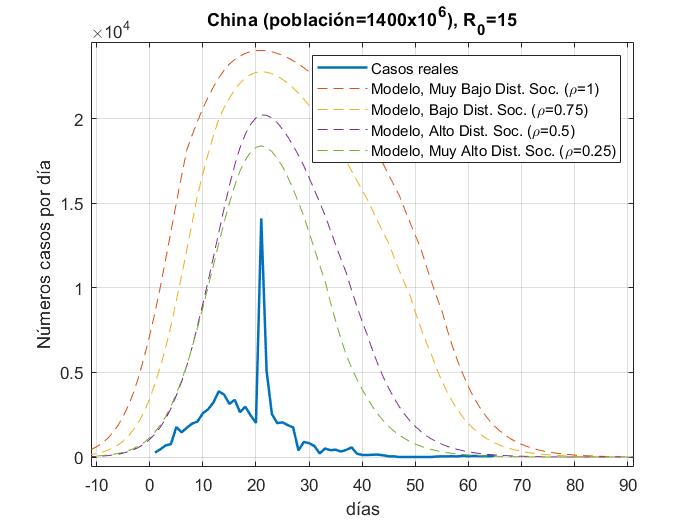
Fig. 4.- Número de casos reales Vs modelo para China con a) R_0=3.5y b) R_0=15
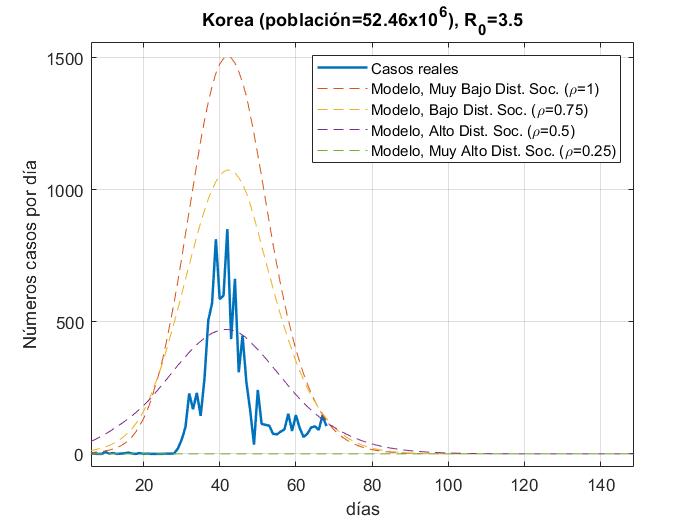
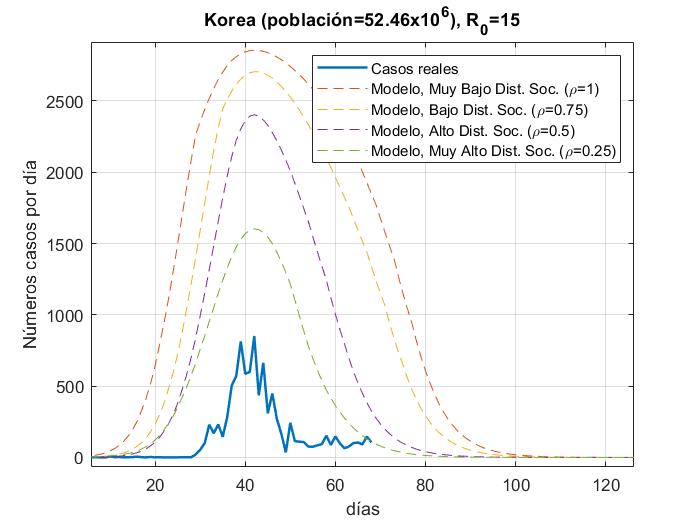
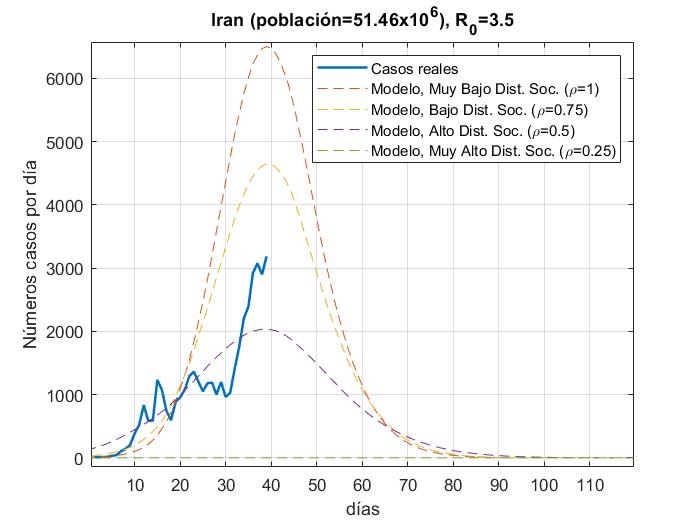
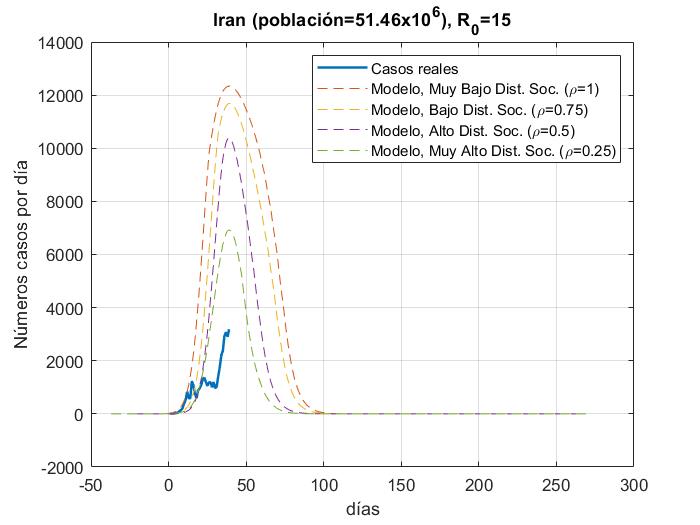
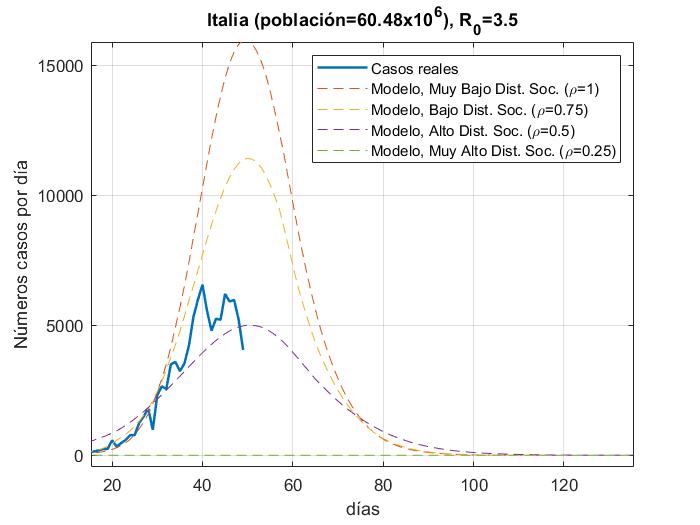
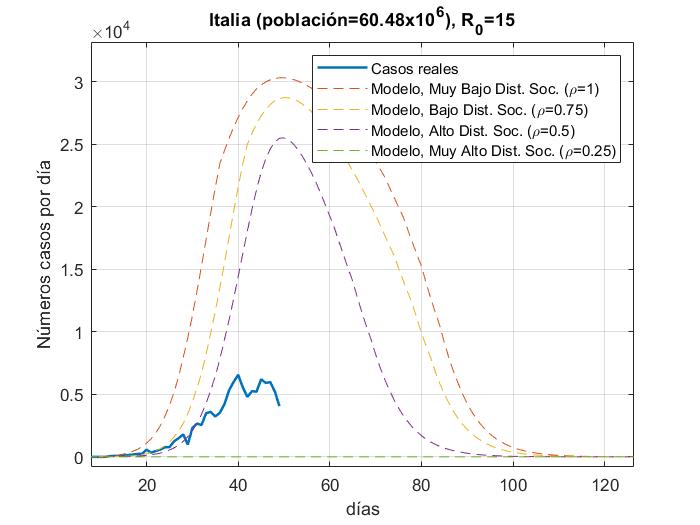
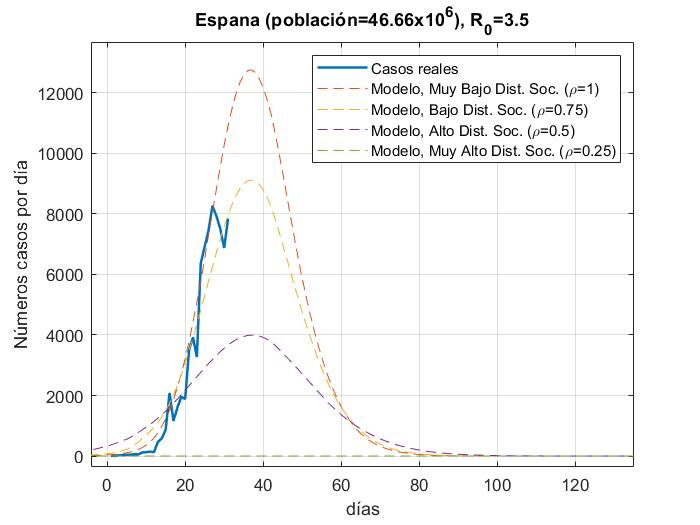
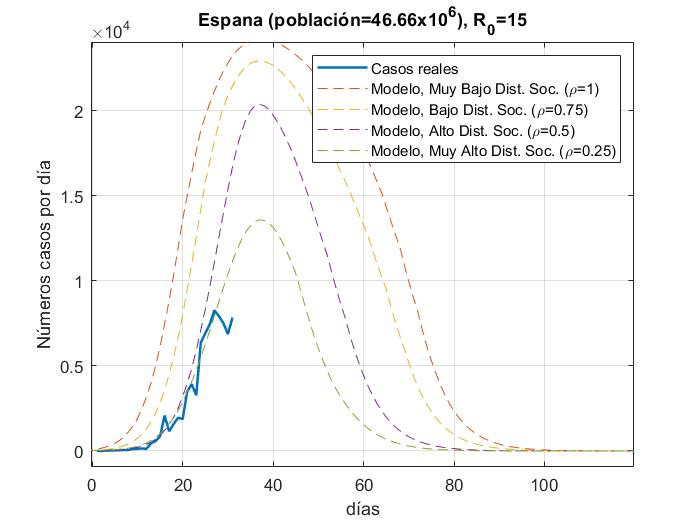
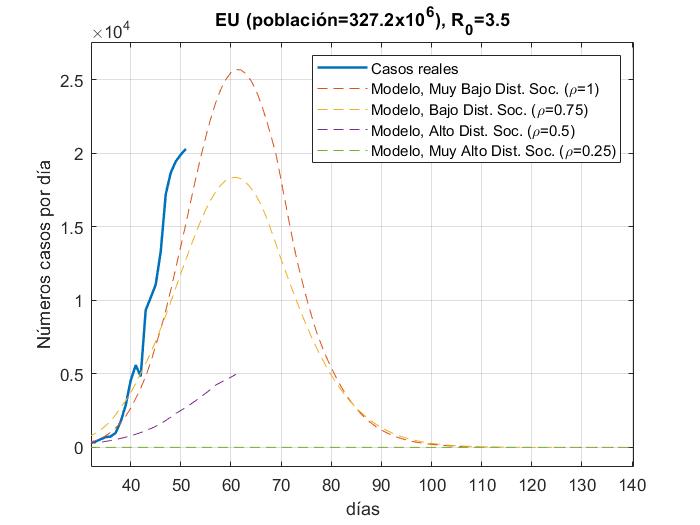
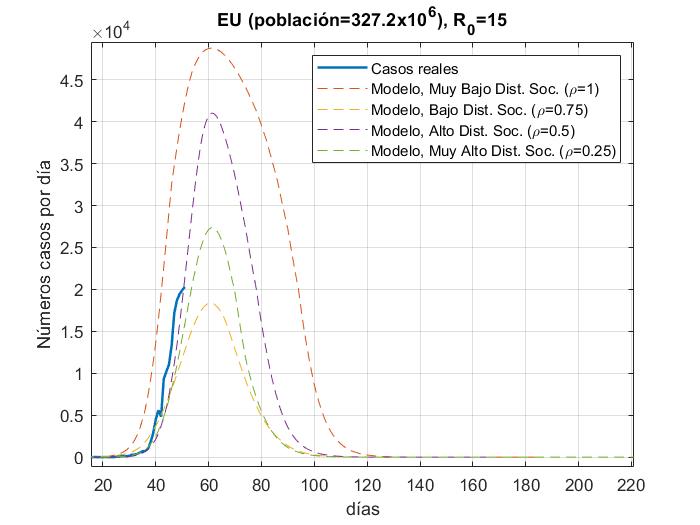
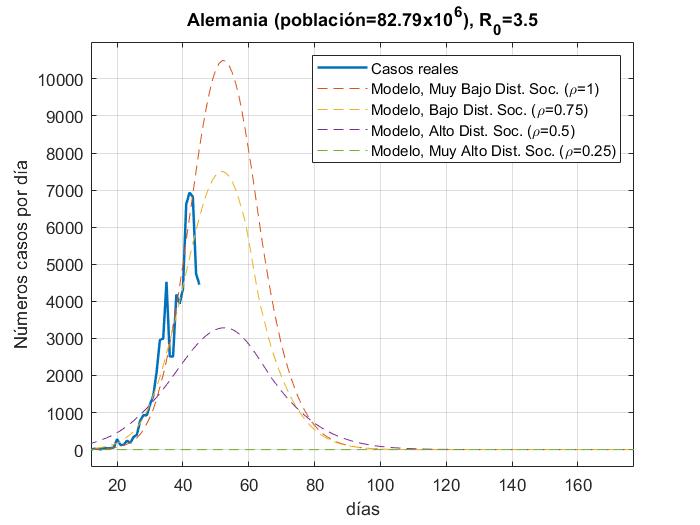
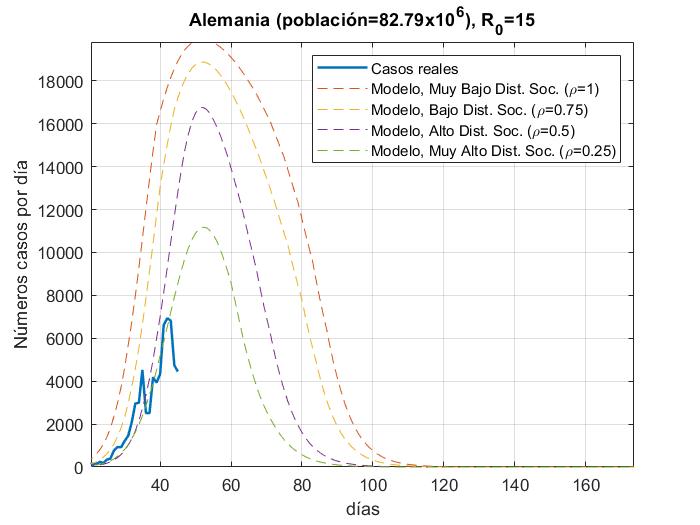
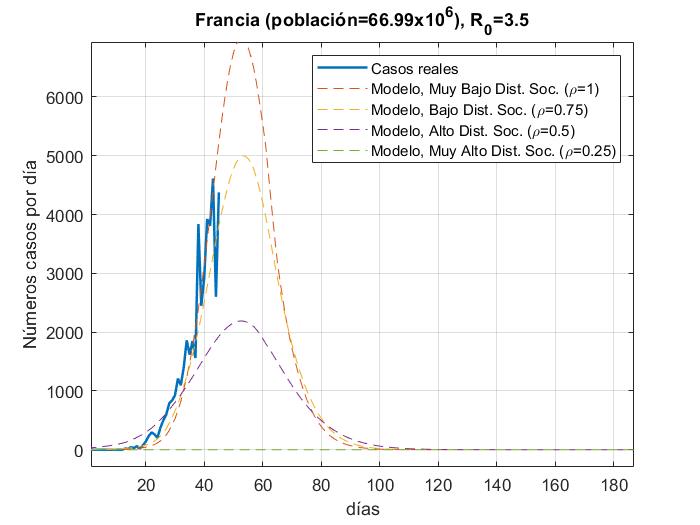
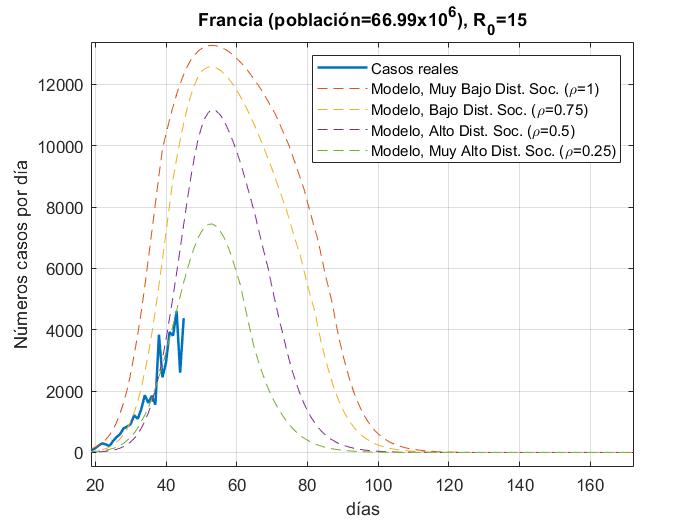
Fig. 11.- Número de casos reales Vs modelo para Frania con a) R_0=3.5y b) R_0=15
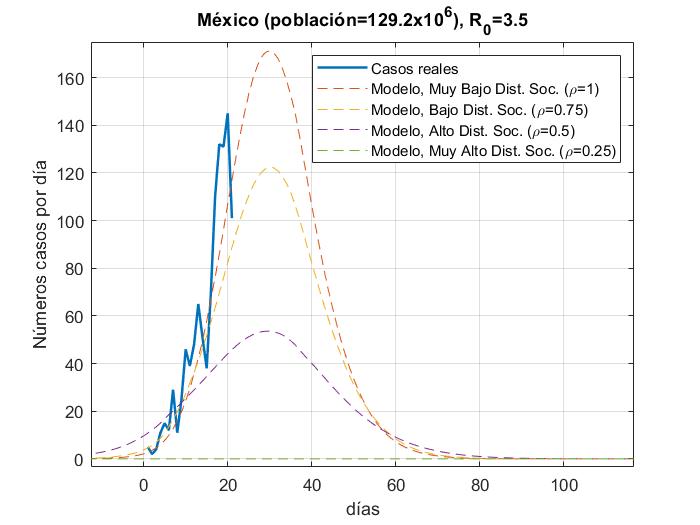
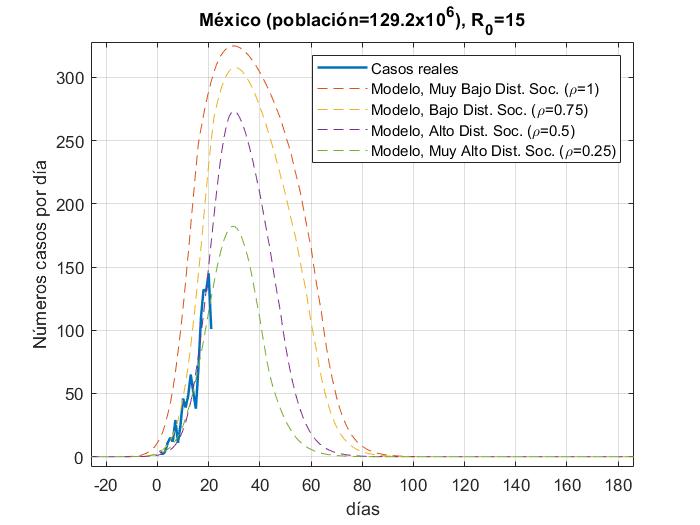
En las figuras podemos observar cómo algunos países se apegan muy bien al modelo para un valor de distanciamiento social dado para R_0=3.5 a excepción de Estados Unidos y España, los cuales tienen una tasa de crecimiento muy alta debido a que su tasa de recuperación es muy baja y para poder ajustar la curva, la propuesta sería elevar el factor de la fuerza de contagio
de R_0=15. Para México es muy temprano para establecer una tendencia de crecimiento de casos, pero podemos ver que la fuerza de contagio ya es mayor a 3.5.
Validación
Para validar estos resultados sólo pudimos hacer la comparación con los datos reales de China y Corea del Sur ya que son los dos países con más casos y ya prácticamente la enfermedad se encuentra controlada. Utilizamos la herramienta matemática de correlación cruzada normalizada obteniendo los porcentajes de parentesco entre el modelo con R_0=3.5 y los datos reales de infectados hasta la fecha de publicación de este artículo y los resultados mostramos en la Tabla 1.
| País | Correlación (%). ρ=1 | Correlación (%). ρ=0.75 | Correlación (%). ρ=0.5 | Correlación (%). ρ=0.25 |
| China | 76.3577 | 76.6594 | 74.5472 | 62.9414 |
| Corea del sur | 85.5470 | 86.8154 | 85.1209 | 74.1682 |
Conclusiones
De acuerdo con los resultados mostrados, se nota claramente que entre mayor sea el factor de distanciamiento social mayor será la mitigación de la curva de infectados. Estas gráficas se pueden tomar como una pauta en la predicción a futuro para los países que aún no llegan a la convergencia o el punto máximo de infectados, pero con un margen de error del 20% o 30% de acuerdo a los resultados de correlación con los datos reales; por ejemplo, para Alemania podemos observar que para el peor de los escenarios (sin distanciamiento social), podría llegar alrededor de los 12000 infectados en un solo día y durar aproximadamente 60 días; para Estados Unidos en el peor de los escenarios podrían alcanzar alrededor de los 32000 infectados en un sólo día y durar hasta 120 días; para México, es muy temprano saber cuál será la tendencia, pero por ahora podrían estimarse alrededor de 250 casos en su día máximo y durar hasta 120 días. Entre más tiempo pase más datos tendremos acerca del comportamiento de la pandemia y el modelo puede ser cada vez más certero.
REFERENCIAS
[1] https://www.who.int/
[2] C. Hubbs, “Social Distancing to Slow the Coronavirus: Modeling the flattening of the COVID-19 peaks,” March 12, 2020.
[3] S. Riley, C. Fraser, C. A. Donnelly et al., “Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions,” Science, vol. 300, no. 5627, pp. 1961–1966, 2003.
[4] G. Chowell and H. Nishiura, “Transmission dynamics and control of Ebola virus disease (EVD): a review,” BMC Medicine, vol. 12, pp. 196–212, 2014.
[5] Y.-H. Hsieh, S. Ma, J. X. Velasco Hernandez, V. J. Lee, and W. Y. Lim, “Early outbreak of 2009 influenza a (H1N1) in mexico prior to identification of pH1N1 virus,” PLoS ONE, vol. 6, no. 8, Article ID e23853, 2011.
[6] F. A. B. Hamzah, et al., “CoronaTracker: World-wide COVID-19 Outbreak Data Analysis and Prediction,” March 19, 2020.
[7] L. Hong, et. al., “Epidemic analysis of COVID-19 in China by dynamical modeling,” Feb. 18, 2020.
[8] S. A. Lauer, Kyra H. Grantz, Qifang Bi, Forrest K. Jones, Qulu Zheng, Hannah R. Meredith, Andrew S. Azman, Nicholas G. Reich, Justin Lessler. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application.Annals of Internal Medicine, 2020; DOI: 10.7326/M20-0504
[9] K. Gander, “How contagious is the new coronavirus, and how does it compare to flu and sars?,”Newsweek, March 20, 2020.
[10] https://www.worldometers.info/coronavirus/
[11] J. He, et. al., “Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions,” Journal of Thoracic Disease, Feb. 27, 2020.
[12] Q. Li et al, “Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia,” The New England Journal of Medicine, pp. 1-9, 2020.